|
��8��
.jpg) �@�@ �@�@.jpg)
�]���A�u�������̑��v�̗̈�Ƃ��Ċ����Ă������e�̂����A�펯���ȊO�ŁA�Ƃ��ɉ������Ă����Ȃ���Ȃ�Ȃ����́A�u�P�D��]�����v�u�Q�D�@�����̗����v�u�R�D���@�̔��v�̂R�ł��B
���̂R�́A�U�̈�̂ǂ����ɓ���悤�Ǝv���Γ��������ł����A�u�ω��̖@������T���o���v�Ƃ����ۑ�ł��̂ŁA���̋��ʍ����ӂ܂��āu�����v�Ƃ��Ă��܂����B���̉ۑ�́A�Ƃ��ɖڐV�������̂ł͂���܂��A�₢�����̎d���ɂ��Ȃ�̍H�v�������܂��B��̓I�Ɍ��Ă����܂��傤�B
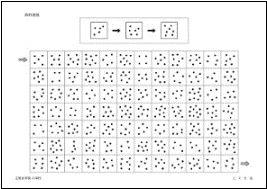
���̖��́A�u��]�����v�̖��ł��B�@�͊ϗ��Ԃ̊�{���ł����A�A�̂悤�Ȉʒu�ړ����Ƃ��Ȃ���]��������܂��B�܂��A�T�C�R�����g������]�������H�v����Ă��܂��B
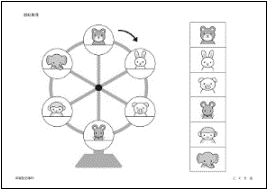
�@��]�����i�w�K�@�����ȁj
�ϗ��Ԃ������������悹�ĉE�ɉ���Ă��܂��B
�E�l�Y�~���P�ԏ�ɗ����Ƃ��A�u�^����̂Ƃ���ɂ͒N�����܂����B�E����I��Ŏw�ł����Ă��������B
�E�l�Y�~���P�ԏ�ɗ����Ƃ��A�T������͒N�̂Ƃ���ɍs���܂����B�E����I��Ŏw�ł����Ă��������B
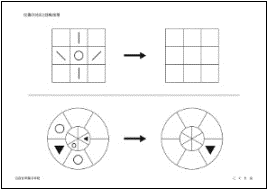
�A�ʒu�̑Ή��Ɖ�]�����i���S���w�����w�Z�j
�E��̂����������Ă��������B���̃}�X�̒��ɂ���`������E�̃}�X�̓����Ƃ���ɂ����Ă��������B
�E���̂����������Ă��������B���́�������āA�傫�������E�̂悤�Ɉړ����܂����B���̌`�͂ǂ��Ȃ�܂����B�E�́��̒��Ɍ`�������Ă��������B
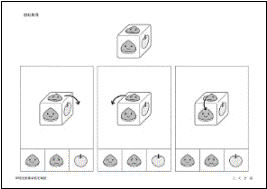
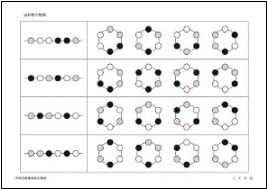
�B��]�����i����c���Ɗw�Z�������j
�E��̃T�C�R�������Ă��������B���Ă���N���̊G�̔��Α��ɂ́A���Ă���N���̊G�������Ă���܂��B�����S�̊G��{���Ă���N���̊G�̔��Α��ɂ����ꂼ�ꓯ���G�������Ă���܂��B���̃T�C�R������̕����ɂP��]�������Ƃ��A�P�ԏ�ɂ͉��̊G�����܂����B���̊G����I��Ő��������Ă��������B
|
���̒��Œ��ӂ��ׂ��_�́A�@�̊ϗ��Ԃł͂Q�Ԗڂ̎���ł��B�܂��A�A�̖��ł́A������]�������̈ʒu�W���ԈႢ�₷���Ǝv���܂��B�B�̃T�C�R���̉�]�ł́A���E�̉�]�����łȂ��A�O��̉�]�������Ă���Ƃ��낪�v���ӂł��B�P���̉�]�ł����炠�܂������ł͂���܂��A���ꂪ������]�������ɂȂ�ƁA���Ȃ������ɕω����܂��B
���ɁA�u�@�����̗����v�Ɋւ�����ł��B�]���u�}�`�n��v�ƌĂ�ł������ł����A�}�`�ȊO�̂��̂��ω�������A������g���Ė��H�Ɏd���Ă��肵�Ă��܂��B�܂��A�u���X���b�h�Ƃ����g�߂Ȃ��̂��g�����A���ѕ��̖@�����̖����o�ꂵ�Ă��܂��B�ȉ������̋�̓I�Ȗ��ł��B
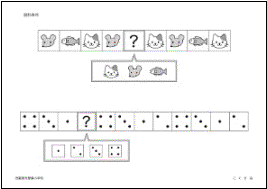
���}�`�n��i�c�����z�ԗt���w�Z�j
�E����ł�����̂̏��Ԃ��l���āA�Ă���u�H�v�̂������ɓ�����̂�������I��Ł������Ă��������B
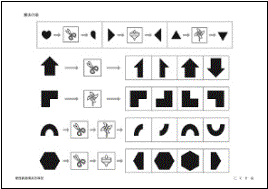
 ���n����H�i�������w�@���w�Z�j ���n����H�i�������w�@���w�Z�j
�E����́�����E���́��܂ŁA��ɂ����Ă��鐔�̏��Ԃ�����Ԃ��āA�����Ђ��Ȃ�����H��i��ł��������B�c�Ɖ��ɂ͐i�߂܂����A�߂ɂ͐i�߂܂���B�����}�X���Q��ʂ��Ă͂����܂���B
���@�����̗����i����c���Ɗw�Z�������j
�U�̃r�[�Y���Ђ��ɒʂ��ău���X���b�g�����܂��B
�E���̂������̃r�[�Y�̂Ђ�������ŗւɂ������̂��E����T���āA�Ԃ��������Ă��������B���ѕ����悭���Ă��������B
|
�Ō�Ɂu���@�̔��v�ƌĂ�ł����̂́A�g���l����ʉ߂���Ƃ���ω����s���A���̖@�������o���đ��̂��̂ɓ��Ă͂߂�Ƃ������̂ł��B���w�Z�̎Z���ɂ�����u�u���b�N�{�b�N�X�v�Ƃ����ۑ�́A���̒��łǂ�Ȍv�Z���s��ꂽ�����l���āA�������o���ۑ�ł��B��ʓI�ɁA���̕ω������߂��܂����A�ŋ߂ł́A���ɏЉ��c��`�m���l�������̖��̂悤�ɁA���ȊO�̕ω����o�ꂵ�Ă��܂��B�܂��A���̖��◧�����w�@���w�Z�̖��̂悤�ɖ������ɗ^�����Ă���ꍇ�ƁA�ԗt���w�Z�̖��̂悤�Ɏ����ŕς���T���������Ɨ�������܂����A��͂�A�����Ō����o�����Ƃ��K�v�Ȗ�肪�ł���悤�ɗ��K���Ă��������B
�����@�̔��i�c��`�m���l�������j
�����炨�������܂�����A�悭�����Ă��������B�n�T�~�̔���ʂ�ƁA�n�T�~�Ő��Č`�������������ɂȂ�܂��B�R�}�̔���ʂ�ƁA�`���R�}�̂悤�ɉ���ĉE�ƍ������ɂȂ�܂��B������܂̔���ʂ�ƁA�`��������܂̂悤�ɉ���āA��Ɖ������ɂȂ�܂��B
�E���̂��ŁA���ɂ���`������ʂ�Ƃǂ̂悤�Ȍ`�ɂȂ�܂����B���ꂼ��E����I��ʼn��́������Ă��������B
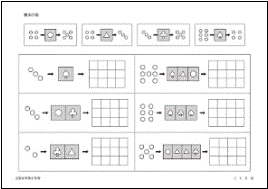
�����@�̔��i�������w�@���w�Z�j
��̂������Ă��������B���̔���ʂ�Ɛ����P�����܂��B���̔���ʂ�ƂP����܂��B�N���[�o�[�̂�������ʂ�ƂQ�����A�X�y�[�h�̔���ʂ�ƂQ����܂��B
�E���̂��ŁA���̂悤�ɍ��̂��̂�����ʂ�ƁA�����ɂȂ��ďo�Ă��܂����B���̐������E�̂������Ɂ��������Ă��������B
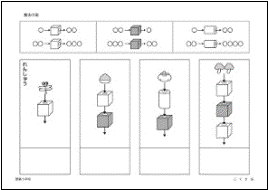 �����@�̔��i�ԗt���w�Z�j �����@�̔��i�ԗt���w�Z�j
��̂����������Ă��������B���̒���ʂ�ƁA�����ς���ďo�Ă��܂��B�ǂ�Ȃ��ŕς���Ă���̂��l���Ă��������B
�܂��A�����̂����������Ă��������B���K���Ă݂܂��傤�B�g���{�P�C����������ʂ�ƁA���C�ɂȂ��ďo�Ă��܂����B���̐��́������̂������ɂ����Ă��������B
�����ł��ˁB�����Ďl�p������ʂ�ƁA�����P������̂ŁA�Q�C�ɂȂ�܂��B�Q�́������������ł��ˁB�E�����Ď�����̖�������Ă��������B
|
�ȏ�A�R�̓T�^�I�Ȗ����Љ�܂������A�����ŏЉ�����́A�K�������V�X���̖�����ł͂���܂���B�̂��炠���Ԃ̂悤�Ȗ�������܂����A���ꂾ���łȂ��A���w�Z���̍H�v�ɑΉ��ł��邾���̗���͂�g�ɂ��Ȃ��Ă͂����܂���B���̂��߂ɂ́A��������������Ă�����悤�ȔS�苭���w�K���K�v�ł��B���������������ނ悤�Ȃ����ł́A�`�̕ς�������ɂ͑Ή��ł��܂���B
.jpg) �@�@�@ �@�@�@.jpg)
�ŐV�@�v��搶�̃R�����͂�����@�i�����܉�HP�@�����̃R�����j
�����܉�ނ͂�����
�֘A�R����
|
| �@�����R�����@��S�U�W���u�w�l����́x�����߂�����̑����v�@������ |
| �@�q�ǂ��͂ǂ��ł܂������Q�X�u�ϗ��Ԃ̖��́u�Ȃ��t�߂�v���Ȃ��Ă͂Ȃ�Ȃ��̂��v�@������ |
|
�������܉�g�s�b�N
�E�����܉�u����̂��ē��v�@������
�E�N�����Ώہu�c��͎��v
�@������
�E�u�����܂Ȃсv�v���W�F�N�g���J�n���܂����@�@������
�E�P�O�O�Ă�L�b�Y�@�V�����u�����p�Y���E���͂����ł����̂��������v�@�@������
�@
|
|
![]()
![]()