|
第3回
.jpg) .jpg)
前回の「未測量」同様、「位置表象」の領域も、小学校入試でたくさん問題が出題されるわけではありません。しかし、出題されると相当難しい問題が出されます。もともとこの領域の問題は、左右関係が絡む、次のような問題が難しい問題として出題されていました。
①他人の右手左手
②方眼上の位置、及び移動
③四方からの観察
④地図上の移動
最近の傾向として、従来からある問題がより洗練されて出題されるだけでなく、論理性や作業性が求められる問題が多く出題されるようになってきました。その一つが「飛び石移動」であり「つみ木を使った四方観察」「回転位置移動」です。具体的に見てみましょう。
飛び石移動は、雙葉小学校で出題された次の問題から始まり、同校で難易度に磨きがかかり、それが最近では、他校で工夫された問題が出題されるようになりました。
 ①位置の移動：飛び石移動（雙葉小学校）
動物たちが飛び石を渡って、向こう側の森へ行こうとしています。
・ネズミが今いるところから、飛び石を１つずつ６回跳んだらどこに着きますか。着いた飛び石に○をつけてください。
・ネズミが６回で着いた場所に、ウサギが飛び石を１つ飛ばしで跳んで行ったら、何回で着くことができますか。その数だけブドウのお部屋に○をかいてください。
・リスが２つ飛ばしで飛び石を跳んで、向こう岸へ渡ります。何回跳んだら着くことができますか。その数だけリンゴのお部屋に○をかいてください。
②位置の移動：旅人算（雙葉小学校）
カエルとウサギとカンガルーが飛び石を跳んでいきます。３匹は一緒に跳びますが、カエルは１つとばし、ウサギは２つとばし、カンガルーは３つとばしで進みます。
・３匹がそれぞれ２回ずつ跳んだとき、カエルとカンガルーの間に飛び石はいくつありますか。リンゴのお部屋に○をかいてください。
・真ん中の飛び石の絵を見てください。カンガルーがゴールに着いたとき、カエルとウサギはどこにいますか。カエルのいる場所に○、ウサギのいる場所に×をつけてください。
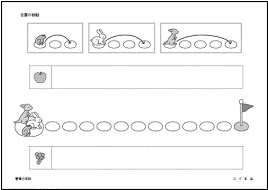 ・カンガルーはゴールまで行ったら、今度は折り返して戻っ てきます。カンガルーとカエルが一緒に跳び始めると、戻ってきたカンガルーがカエルに会うのは、はじめから数えると、何回跳んだときですか。その数だけブドウのお部屋に○をかいてください。
３．位置の移動：飛び石移動（聖心女子学院初等科）
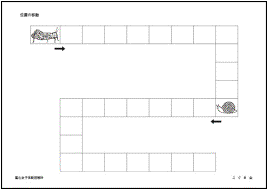 バッタとカタツムリがマスの中を矢印の方に進みます。バッタは３つとばしで４つずつ進みます。カタツムリは１つずつ進みます。
・２匹が一緒に進んだとき、同じところに着いた場所に青で ○をかいてください。
また元の場所に戻ります。今度はお約束が変わります。バッタは１つずつ進みます。カタツムリは１つ進んだら、１回休みます。
・このお約束で２匹が一緒に進んだとき、同じところに着いた場所にエンピツで○をかいてください。
|
とくにこの問題では、２つ以上のものが同時に動く２や３の問題は、明らかに将来高学年で学ぶ「旅人算」の考え方が根底にあります。作業を通して考えさせる典型的な問題です。こうした問題の解決法は、実際に自分でコマを動かしてみる経験が大事です。１つのコマを動かすことをまず練習してから、２つのコマを動かす練習をしてください。とくに２つのものを動かす場合の動かし方には工夫が必要です。
次に、最近沢山の問題が見られるのは「つみ木を使った四方からの観察」です。従来からこの問題は、位置表象領域の中で、もっともよく出題されていた典型的な入試問題ですが、その出題がだんだん少なくなりました。２０１２年度あたりからまた急に出題されるようになり、それも「つみ木」を使った出題が沢山見られました。この問題は、ピアジェの認識心理学における「思考実験」の一つですが、そのほとんどが具体物を使った出題でした。それが各学校申し合わせたようにつみ木を使い始めました。つみ木ですと、四方からの見え方だけでなく、上から見たら・下から見たら（透明の板に乗せて下からのぞく）というように上下が加わり、「六方からの観察」になっています。その変遷をみると次のようになります。
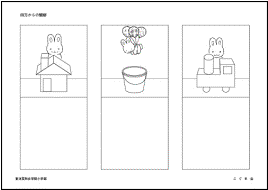 ①四方からの観察：絵で描く（東洋英和女学院小学部）
ウサギが、いろいろな方向からテーブルの上のものを見ています。
・ウサギから見たら、お家はどのように見えますか。下のお部屋に絵をかいてください。
②四方からの観察：具体物を四方から見た見え方（光塩女子学院初等科）
テーブルの上のものを４人のお友達が見ています。これから、みんな自分の左のお椅子に移ります。メガネの子からテーブルのものはどう見えますか。右の絵から選んで△をつけてください。
またその時、クマの髪どめをした子からはどう見えますか。○をつけてください。
③四方からの観察：つみ木を使った問題（白百合学園小学校）
・ネコさんのところから、つみ木を見るとどう見えますか。下のお部屋に△をつけてください。
・タヌキさんのところから、つみ木を見るとどう見えますか。下のお部屋に×をつけてください。
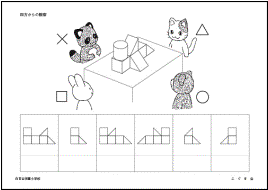
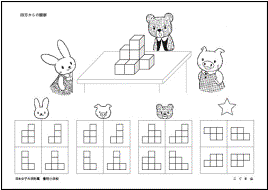
④四方からの観察：上から見た時も問うつみ木の問題（日本女子大学附属豊明小学校）
・それぞれの動物から見たときのつみ木の見え方はどれですか。下のお部屋から選んで水色の○をつけてください。
・正面に立って真上から見たとき、つみ木はどのように見えますか。☆のお部屋から選んで水色の○をつけてください。
|
これからもいろいろ工夫された問題が出題されると思いますが、具体物であれ、つみ木であれ、実際の場面を作って、自分で実際に描いてみるという経験をたくさん積ませることがまず何よりも大事です。最初からペーパーに取り組むような勉強法では、ものごとの見方が身に付きませんし、新しい問題に対処できません。
さて、「回転推理」に関する問題は、「観覧車」がその典型ですが、それ以外にもいろいろな問題が工夫されて出題されています。とくに図形課題と結び付くことが多く「回転図形」として多く出題されていますが、それ以外のものも多く「回転位置移動」として取り組んでいます。
①回転推理（雙葉小学校）
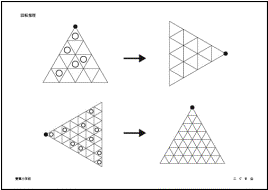
左の三角が回転して右のようになったら、中の○はどうなりますか。右の三角の中に○をかいてください。
②回転推理（白百合学園小学校）
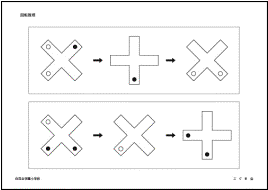
左にある形が回っていきます。真ん中と右の形の足りないところに、それぞれ●や○をかき足してください。
|
回転の要素を取り入れた問題は、とくに図形領域に多く見られます。その意味でも「回転」は、現在行われている入試の一つの「キーワード」かもしれません。
以上３つの新傾向の問題を紹介しましたが、この他にも「話の内容理解の中における地図上の移動」等も注目しておく必要があります。いずれにしても、昔から「左右関係の理解」が位置表象の中心であることには変わりませんので、よく練習してください。
.jpg) .jpg)
最新 久野先生のコラムはこちら （こぐま会HP 室長のコラム）
こぐま会教材はこちら
関連コラム
|
| 室長コラム 第４０５号「なぜ「四方からの観察」がよく出題されるのか」
こちら |
| 室長コラム 第２３１号「ペーパーのみの学習では思考力は育たない」 こちら |
|
☆こぐま会トピック
・年長児対象 こぐま会ひまわり会「室長特別講座 夏季トレーニング」 こちら
・年長児対象「合格判定テスト」
こちら
・年長児対象「入試対策クラス ステップＥ」 こちら
|
|
ページトップへ