|
��2��
|
�@�����ʗ̈�ɂ�����V�X���̖�� |
.jpg) �@�@ �@�@.jpg)
�u�����ʗ̈�v�ɂ�����������́A�̂��炻��قǑ����o�肳��Ă����킯�ł͂���܂���B�u�V�[�\�[�v�̖��ɑ�\�����u�W�����v�����̗̈�̒��S�ۑ�ł����B�������N�A�V�����ۑ肪�������킯�ł͂���܂��A����܂ł������P���ȁu�V�[�\�[�v�̖���u�肠���v�̖��ɐV�����v�f�������A�V�X���̖����`�����Ă��܂��B�ŋߏo�肳�ꂽ���̒�����A�q�ǂ������ɂƂ��Ă�����V�X���̖������������Љ�܂��傤�B�V�����`���̖��́A���̂S�̒P���Ō����܂��B
�P�D�V�[�\�[
�Q�D�肠��
�R�D�ʒP��
�S�D�t�Ή�
�܂��A�ŏ��ɃV�[�\�[�̖��ł��B
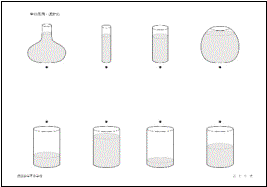
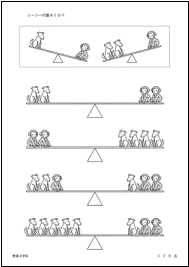 ���V�[�\�[�̏d������ׁi�ԗt���w�Z�j ���V�[�\�[�̏d������ׁi�ԗt���w�Z�j
�P�ԏ�̂������̃V�[�\�[���悭���Ă��������B
�C�k�P�C�ƃT���P�C������ׂ�ƃT���̕����d���A�C�k���Q�C�Ȃ�T���P�C�����C�k�̂ق����d���Ȃ��Ă��܂��B
�ł́A���̃V�[�\�[�̂悤�ɏ悹��Ƃǂ��Ȃ�ł��傤�B�V�[�\�[�̉�����ق��Ɂ������Ă��������B
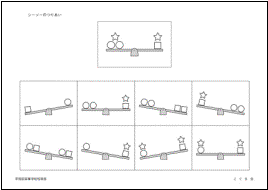 ���V�[�\�[�̂肠���i����c���Ɗw�Z�������j ���V�[�\�[�̂肠���i����c���Ɗw�Z�������j
��̂������̃V�[�\�[�͂肠���Ă��܂��B
���̃V�[�\�[�̏d���̊W���悭���Ă��������B
���̂�������̃V�[�\�[�̒��ŁA��̃V�[�\�[�̊W�ƍ����Ă��Đ��������̂Ɂ������Ă��������B
�V�[�\�[�̊�{���́A�R�ҊW�̗�������{�Ƃ��āA�S�ҁE�T�ҊW�܂Ŕ��W����d������ׂł��B�d�����ɕ��ׂ���A���Ԗڂɏd�����̂�T�����肷��ۑ�ł����A�����ɏЉ���ԗt���w�Z�̖��́A�₢�����̎d�����Ⴂ�܂��B�T���ƃC�k�̊�{�I�ȏd���̊W�����āA���̂S�̃V�[�\�[�̂ǂ��炪�����邩�Ƃ������ł��B��̂Q�̓Z�b�g�̍l�����A���̂Q�͗������瓯�����̂����낷�i�����j�Ƃ��������w�K����u�����Z�I���z�v�����p���Ă��܂��B�E�ƍ����瓯�����̂����낵�Ă��d���̊W�͕ς��Ȃ��Ƃ������Ƃ��ǂ������ł��邩���|�C���g�ł��B
�܂��A����c���Ɗw�Z�������̖��ɂ͂Q�|�C���g������܂��B�P�́A��{�ƂȂ�u�肠���Ă����ʁv�ŗ����ɐ�������܂��B���̐��𗼕����牺�낵�Ă��W�͕ς��Ȃ��Ƃ������Ƃ�������ǂ����ł��B�����ĂQ�ڂ́A�c�������Q�Ɓ��P���肠����Ԃ����āA���P�Ɓ��P�Ƃł͂ǂ��炪�d�����𐳂������f�ł��邩�ǂ����ł��B���X�A�Q���遛�̕����P�ɂȂ��Ă��d���ƍl���Ă��܂��q�ǂ��������܂��B�u�Q�v�Ƃ������Ɉ�������ꂽ���ʂł��傤�B���̂Q�_�̗������������蓥�܂���A���̃V�[�\�[�Ő��������̂ƁA�Ԉ���Ă�����̂̔��ʂ͂ł���͂��ł��B���̂悤�ɁA�]�����炠��u�d�����n����v���ł͂Ȃ��A�u�_���v��K�v�Ƃ����肪�o�n�߂Ă��܂��B
�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E
���Ɂu�肠���v�Ɋւ�����ł��B
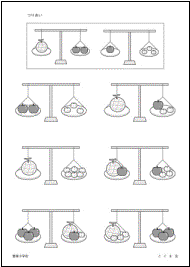
���肠���i�ԗt���w�Z�j
��̂����������Ă��������B�ʕ����悹���Q�̓V���͂肠���Ă��܂��B
�ł́A���̂悤�ɉʕ����悹����ǂ��Ȃ�ł��傤���B
�肠�����̂Ɂ��A�肠��Ȃ����̂Ɂ~�����Ă��������B
���̙ԗt�̖��̏����̎d���́A�̂��炠��ʂ�ł��B���Ȃ킿�u�`���Q�a�E�a���R�b�v�Ƃ����W�ł��B�������ݖ�́A�肠�����߂̐����L���̂ł͂Ȃ��A�u�肠�����́v�Ɓu�肠��Ȃ����́v�ʂ�����ɂȂ��Ă��܂��B���ł��]���̖��ƈႤ�̂́A���i�E���Ɖ��i�����̓V���̂悤�ɁA�����ɓ��������S������Ă���Ƃ����_�ł��B���̂܂c���āA�u�����������Ȃ��獶�E�̊W�𗝉����邩�A��قǂ̃V�[�\�[�̖��̂悤�ɁA���������S�����낵�Ă���c�������̂ōl���邩�́A�ǂ���ł��ǂ��̂ł����A�������Ȃ������l���₷���Ƃ�����A�������瓯�����̂����낵�Ă��W�͕ς��Ȃ��Ƃ������@���g���̂��悢��������܂���B���̂悤�ɁA�����Ő����������ނ����łȂ��A�u�����������Ȃ���f����Ƃ������͍��㑝���Ă����ł��傤�B�^�ʂ�̖��łȂ��Ă������Ă����邾���̉��p�͂�g�ɂ��Ȃ��Ă͂Ȃ�܂���B
�R�Ԗڂ́u�ʒP�ʁv�Ɋւ�����́A�ŋߑ����Ă�����ł��B���Ƃ��ƒP�ʂ̊w�K�́A���w�Q�N���ŁA�����A�d���A�������̒P�ʂ̊w�K�����܂��B�������甭�W����P�ʊ��Z�̖��́A��w�N�̎q�ǂ������ɂƂ��āA���Ȗ��̈�ł��B�Ⴆ�A�����ł���A���[�g���E�Z���`���[�g���A�~�����[�g���̊W����������c�����Ȃ��ƒP�ʊ��Z�ł܂Â��Ă��܂��܂��B�����������w�Z�Ŋw�ԒP�ʂ́u���ՒP�ʁv�ƌĂ�ł��܂����A�P�ʂ̍l�����́A���̂悤�ɂS�̒i�K���o�Đ������Ă����܂��B
�@���ڔ�r�E�E�E�E���ڂ���ׂ�
�A�Ԑڔ�r�E�E�E�E������̂𒇗����Ƃ��Ă���ׂ�
�B�ʒP�ʁE�E�E�E������̂��u�P�v�Ƃ��āA���ꂪ���������邩���l����
�C���ՒP�ʁE�E�E�E���E���ǂ��ł��ʗp����P�ʂł���ׂ�
���ՒP�ʂ͏��w�Z�����ɂ͏o�肳��܂��A�ʒP�ʂ̍l�����܂ł͕p�o���Ă��܂��B
�Ⴆ�A���̂悤�Ȗ��ł��B
 ����������ׁi�������q�w�@�����ȁj ����������ׁi�������q�w�@�����ȁj
��̂����������Ă��������B
���ꂼ��̑������Ɠ��������̂��̂�������T���ē���������Ă��������B

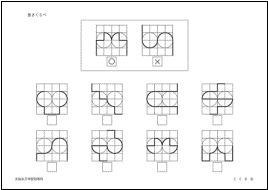
���L������ׁi�ʒP�ʁj�i���S���q�w�@�����ȁj
���̂���{�����Ă��������B�����Ƃ���ƍ����Ƃ���͍L���������ł��B
�ł́A�E�̌`�̒��Ŕ����Ƃ���ƍ����Ƃ���̍L�����������̂�T���āA�������Ă��������B
�������q�w�@�����Ȃ̖��́A�����`�̈�ӂƁA�~���̂P�^�S�i�l���̈�j�̒����̋Ȑ����A���������邩���l���āA���������̂��̂�T���ۑ�ł��B�܂��A���S���q�w�@�����Ȃ̍L����ׂ̖��́A����`���u�P�v�P�ʂƂ������A���ꂪ���������邩���l���A�L��������ׂ���ł��B�����I�ɔ��f�ł���ꍇ������܂����A�����`��Ή��Â��Ă������f���܂��B�K���������̂悤�ɁA�ЂƂ̌`���u�P�v�P�ʂɂȂ�Ȃ��ꍇ������܂����A����������ׂ������߂čl����u�ʒP�ʁv�̍l�������A���w�Q�N���ȍ~�n�܂�u���ՒP�ʁv�̊w�K�ɂȂ����Ă����̂ł��傤�B���̈Ӗ��ő�ϗǂ���肾�Ǝv���܂��B
�Ō�́A�t�Ή��̖��ł��B�̂��獻�����̔Z���̖���A�c��������������̗ʂ𐄗����n����悤�Ȗ�肪�悭�o�肳��Ă��܂��B�����ɏЉ�锒�S���w�����w�Z�̖��́A�ʂ̈ڂ��ւ��̖��ł��B
 ���ʂ̌n��E�t�Ή��i���S���w�����w�Z�j ���ʂ̌n��E�t�Ή��i���S���w�����w�Z�j
�E�Q�Ԗڂɑ����W���[�X�������Ă�����ꕨ����̒�����T���āA�������Ă��������B
�E���̓��ꕨ�ɓ����Ă���W���[�X���ǂ�������ʂɂ���ɂ́A��̂ǂ̃W���[�X�ƍ��킹����悢�ł����B�����т��Ă��������B
���ꕨ�ɓ����Ă���W���[�X���A�ǂ�������ʂɂ���ɂ́A��̂ǂ̃W���[�X�����ꂽ��悢�����Ă�����ł��B�����Ă���ʂ���ԏ��Ȃ���A�P�ԑ�������Ȃ��Ă͂Ȃ�Ȃ����A�Q�Ԗڂɏ��Ȃ������Ă���Q�Ԗڂɑ�������Ȃ��Ă͂Ȃ�Ȃ��E�E�E�E�Ƃ����u�t�Ή��v�̊W�܂��Đ����тł��邩�ǂ����ł��B���X�A�ʂ̑������̓��m����Ή��Â��Ă��܂��ԈႢ�������܂��B�܂��A�t�Ή��̖��ł͂���܂��A�������̔Z�����e�[�}�Ƃ����ȉ��̂悤�Ȗ����o�肳��Ă��܂��B
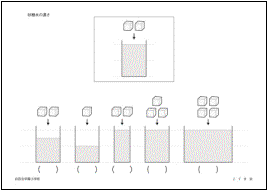 ���������̔Z���i���S���w�����w�Z�j ���������̔Z���i���S���w�����w�Z�j
��̂����������Ă��������B���ꂩ��R�b�v�̐��Ɋp�������Q����Ă��������܂��B
���̃R�b�v�̒��ŁA��̃R�b�v�Ɠ����Â��̍������ɂȂ���̂Ɂ������Ă��������B
�������̔Z�������߂�u�����̌��Ɛ��̗ʂƂ̊W�v�̒��ŁA���̗ʂ��Q�{�ɂȂ�����̌����Q�{�ɂ���A�܂����̗ʂ������ɂȂ�A�����̐��������œ����Â��ɂȂ�Ƃ������Ƃ������邩�ǂ����A�V�������z�̖��ł��B
�ȏ�̂悤�ɁA�����ʗ̈�̖��́A���܂葽���͏o�肳��܂��o�肳�����͓���A���̂��Ƃ�_���I�ɍl���Ȃ��Ă͂Ȃ�Ȃ���肪�����̂������ł��B�V�[�\�[�̖��𒆐S�ɏ\�����K���A�V�����`�̖�肪�o�肳��Ă������̗͂ʼn����Ă�����悤�A��{�ƂȂ���̂̌�������������g�ɂ��A���낢��ȃ^�C�v�̖��ɒ��킵�ĉ��p�͂����Ă��������B
.jpg) �@�@�@ �@�@�@.jpg)
�ŐV�@�v��搶�̃R�����͂�����@�i�����܉�HP�@�����̃R�����j
�����܉�ނ͂�����
�֘A�R����
|
| �@�����R�����@��S�S�X���u�V�X���̖��ɒ�����v
�@������ |
| �@�q�ǂ��͂ǂ��ł܂������@��P�S���u�P�ʂ̍l�����͑厖�ł��v�@������ |
|
�������܉�g�s�b�N
�E�����܉�u�ċG�u�K��v�@������
�E�ی�ґΏ� �����܉��\�Z�~�i�[
�@
�@�V�X�����ւ̃A�v���[�`�̎d���Ɖċx�݂̌��ʓI�Ȋw�K�@
�@������
�E�����܉�u�̌����Ɓv�@�@������
�@
|
|
![]()
![]()