 |
最近の数に関する問題は、どのような傾向なのでしょうか。また、何を重点的に学習したらよいのでしょうか。
|
 久野泰可先生からの回答 久野泰可先生からの回答
小学校受験において、出題される内容をいくつかの領域に分けてみると、やはり「数」に関する出題が多いことがよく分かります。ただし、最近はどちらかというと「図形」に関する出題内容に、学校側は力を入れているようにも思いますが、「数」が小学校受験の中心課題であることに間違いはありません。数に関する幼児向けの教科書があるわけではありませんので、実際に出された問題をどう分析したらよいかは独自に考えなくてはなりませんが、小学校以降の学習内容と関連づけて整理するのが一番分かりやすいし、学習の計画が立てやすいと思います。
小学校以降の算数科の指導内容は、4つの柱「数と計算」「量と測定」「図形」「数量関係」で構成されています。なかでも、入試で「数と計算」の課題につながる出題が多いのは、当然なことだと思います。
現在、小学校における計算の学習は、1年で足し算・引き算、2年で掛け算、3年で割り算と3年間かけて四則演算を学習しますが、小学校入試では、計算そのものは出題されませんが、計算の基礎となる考え方は、四則演算全てにおいて出題されています。つまり「掛け算」も「割り算」もその考え方に関しては、すべて出題されると考えておく必要があります。
数式こそ出されませんが、そのことがかえって問題を難しくしています。いわゆる小学生の苦手な「文章題」の形をとって、お話として出題されるため、聞く力・暗算能力が相当求められています。
では、入試問題をどのように分析し、学習計画を立てればよいのでしょうか。幼児期における数の基礎教育は、将来の算数科につながる内容と関連づけて、次のように考えておく必要があります。
|
1. 集合数の基礎 分類
2. 順序数の基礎 系列化
3. たし算の基礎 分類計数・数の合成
4. ひき算の基礎 数の構成・一対一対応
5. かけ算の基礎 一対多対応 (*)
6. わり算の基礎 等分・包含除
7. 四則演算総合 数の増減・数のやり取り・数の複合問題
(*)一対多対応はかけ算の考え方の基礎ですが、この耳慣れない言葉は、「ひとりでとっくん」を作成する際に「一対一対応」に準じて、久野が作った造語です。 |
7つの項目で、入試問題を整理しましたが、以前は、将来の足し算・引き算につながる内容が、出題の中心でした。
最近の工夫された問題においては、掛け算や割り算の基礎になる「一対多対応」の考え方を応用する問題が、かなり増えています。この「一対多対応」の学習の基礎は、例えば、数人のお客さんに数個ずつ物をあげる数を求める問題と、乗り物のタイヤに注目してタイヤ全部の数を問う問題ですが、実際の入試問題はより工夫されていて「交換」の問題や「つりあい」の問題にまで発展しています。また、他の数の操作と重なり合って、いわゆる「複合問題」の多くがこの「一対多対応」を使って解かなくてはならないようになっています。
では、入試問題の中から「一対多対応」に関する問題をいくつか紹介しましょう。前回も紹介した、ハンバーガーの問題や、絵本2冊と同じ値段のものを探す問題等はその典型ですが、それ以外にも問題は沢山あります。
|
◆白百合(2004年度) 一対多対応と聞き取り
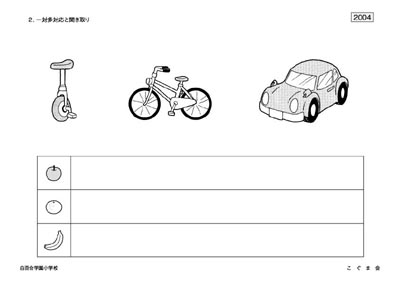
・一輪車3台と自動車2台では、タイヤの数は全部でいくつですか。その数だけリンゴのお部屋に○をかいてください。(11個の○)
・一輪車4台と自動車1台、自転車2台では、タイヤの数は全部でいくつですか。その数だけミカンのお部屋に○をかいてください。(12個の○)
・一輪車2台と自動車3台、自転車1台では、タイヤの数は全部でいくつですか。その数だけバナナのお部屋に○をかいてください。(16個の○)
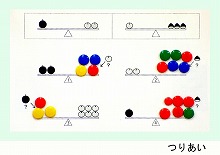
◆暁星(2012年度) つりあい
上のお部屋を見てください。リンゴ1個とミカン3個はつりあいます。ミカン1個とイチゴ2個はつりあいます。
・下のお部屋のようにシーソーの左側に果物を乗せました。反対側にどのように果物を乗せるとつりあうでしょうか。右から選んで○をつけてください。 (上段から:ミカン6個に○、イチゴ6個に○、ミカン12個に○、ミカン2個に○、リンゴ1個に○)
◆聖心(2010年度) 置き換え・重さくらべ
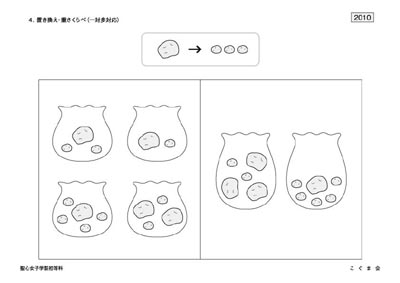
袋の中に、大きいジャガイモや小さいジャガイモが入っています。
・左のお部屋を見てください。大きいジャガイモ1個は、小さいジャガイモ3個と同じ重さです。この中で1番重い袋に青い○をつけてください。(右下に○)
・右のお部屋を見てください。右の袋を、左のジャガイモの入った袋と同じ重さにするには、小さいジャガイモがあといくつ必要でしょうか。袋の中にその数だけ青い○をかいてください。(3個の○)
◆雙葉(2004年度) 一場面の複合問題
3つのベンチに男の子と女の子が何人か座っています。2つのベンチには3人ずつ、1つのベンチには1人が座っています。
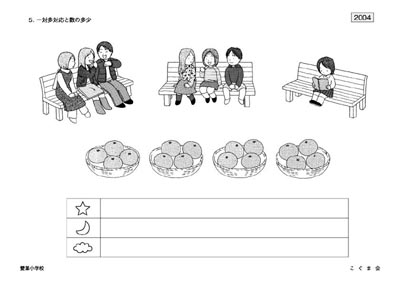
問1.下のカゴのミカンを、1人に2個ずつあげると、ミカンはいくつあまりますか。その数だけ下の星のお部屋に○をかいてください。(2個の○)
問2.新しく女の子がもう1人やってきて座りました。カゴのミカンを女の子全員に3個ずつ配るには、ミカンはいくつ足りませんか。その数だけ月のお部屋に○をかいてください。(2個の○)
問3.最初にベンチに座っていた人の数で考えてください。男の子にも女の子にもミカンを3個ずつあげるとき、男の子と女の子のミカンの数はいくつ違いますか。その数だけ雲のお部屋に○をかいてください。(9個の○)
|
以上紹介した問題のように、「一対多対応」の考え方を応用した問題が、最近の数の領域における新傾向の問題を形成しています。また、シーソーにおける「つりあい」も、重さ比べの問題ではありますが、「一対多対応」の考え方を応用すれば、簡単にできる問題です。
入試問題はいろいろな形をとりますが「一対多対応」の考え方は、「お客さん」の問題と「タイヤ」の問題が基礎になりますので、そこで考え方の基本をしっかり身につけてから、応用問題の練習に入るのが一番良い学習法です。また、掛け算の考え方を裏返せば、割り算の考え方につながりますので、掛け算と割り算の考え方はセットで学習するのがよいでしょう。
 

最新 久野先生のコラムはこちら (こぐま会HP 室長のコラム)
こぐま会教材はこちら
推薦コラム
|
| 室長コラム 第332号 一対多対応の基礎学習
こちら |
| 子どもはどこでつまずくか(31)
こちら |
|
☆こぐま会トピック
・(年中児保護者対象)来年秋に受験される方のために「こぐま会代表セミナー 幼児期の基礎教育と小学校受験」
こちら
・大森校(年長児と保護者対象)「セミナー365&チャレンジテスト365」
こちら
|
|

