 |
最近は少ないペーパーの中で、「考える力」を問う問題が多くなったと聞きますが、その対策はどうしたら良いでしょうか。
|
 久野泰可先生からの回答 久野泰可先生からの回答
最近の小学校入試は、以前と比べてペーパー試験の枚数が少なくなりました。多いところでも10枚前後、平均的には6〜7枚だろうと思います。その少ないペーパーで、学力の基礎を見ようとしているのですから必然的に、訓練で身につくような知能検査的な問題はほとんど出されていません。
どの学校もいろいろ工夫し、子どもたちの「考える力」がどれだけ身についているかを見ようとしています。考える力を求める問題がすべて難問かというと、必ずしもそうでもありませんが、子どもたちにとっては初めての問題が多く出されています。
どんな問題か、具体例を紹介しましょう。
|
☆雙葉小学校
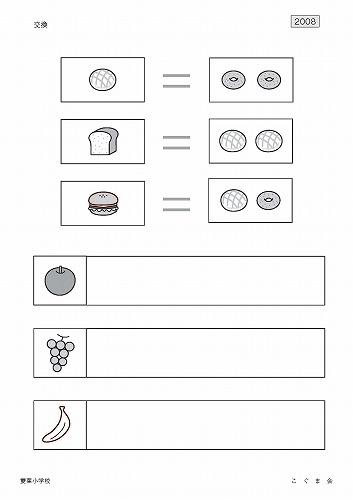
【交換】 (2008年度)
上のお部屋を見てください。
メロン1個は、ドーナツ2個と換えてもらえます。
食パン1斤は、メロンパン2個と換えてもらえます。
ハンバーガー1個は、メロンパン1個とドーナツ1個と換えてもらえます。
・メロンパン4個は、食パンいくつと換えてもらえますか。その数だけリンゴのお部屋に○をかいてください。
・食パン2斤は、ドーナツいくつと換えてもらえますか。その数だけブドウのお部屋に○をかいてください。
・ハンバーガー4個は、食パンいくつと換えてもらえますか。その数だけバナナのお部屋に○をかいてください。
☆聖心女子学院初等科
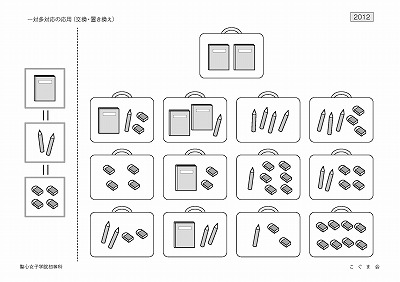
【一対多対応の応用(交換・置き換え)】 (2012年度)
左側の絵を見てください。
絵本1冊と、鉛筆2本、消しゴム4個は、同じ値段です。
花子さんは絵本を2冊買いました。
・絵本2冊と同じ値段で買えるものが入っているカバンを、下から探して青い○をつけてください。
☆白百合学園小学校
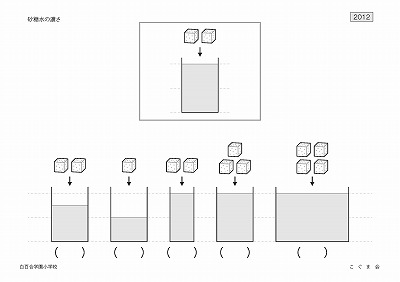
【砂糖水の濃さ】 (2012年度)
上のお部屋を見てください。
これからコップの水に角砂糖を2個入れてかき混ぜます。
・下のコップの中で、上のコップと同じ甘さの砂糖水になるものに○をつけてください。
|
少し解説をしてみましょう。
雙葉小学校の交換の問題は、この学校で昔から出されていた流れを引き継ぎ、問題がより難しくなっています。最後の「ハンバーガー4個は食パンいくつと換えてもらえますか」という問題が難しいのですが、その理由は一種類のものが二種類のものと変えてもらえるという条件が問題を複雑にしているからです。そしてもう一つ基礎的なことですが、例えば食パンとメロンパンの関係において、食パンからメロンパンの数を聞く場合(掛け算の考え方)と、メロンパンから食パンの数を聞く場合(割り算の包含除)の両方が理解できなければいけないという点です。
子どもの思考は一方通行になりがちですので、食パンからメロンパンの数を聞けばできるものが、メロンパンから食パンの数を問われると分からなくなってしまう子が大勢います。逆から考えることの大切さは、ここでもはっきり表れています。そのため、最後のハンバーガーの問題でも「3」という正解のほかに、「2」であったり「4」であったり、いろいろな解答が出てきますが、どれも間違いの理由があるのです。例えば、「2」と答えた子は、メロンパン4個を食パン「2斤」に換え、残りのドーナツは食パンと換える約束がないから、手をつけていないのです。また、「4」と答えた子は、4個のドーナツを2個ずつのかたまりにし、そのかたまりが2個できるので、メロンパンから換えた2個と合わせて4個としているのです。ドーナツを変えた2個がメロンパンであり、それをもう一度食パンに変えなくてはならないのに、その交換作業をやっていないのです。もう一歩のところで誤答になっていますが、考える道筋は間違っていません。
この問題は、「交換」の代表的な問題として、よくセミナー等で話題にしてきましたが、この問題を出題した学校側は、何を求め、またどんな能力を身につければこの問題を解くことができるのか、そこをしっかり分析しておかなければなりません。もともと雙葉小学校では、昔から数に関する出題において、掛け算や割り算の考え方につながる「一対多対応」の問題をよく出題してきましたが、今回ご紹介したこの問題は、その中でも難易度において最高レベルの問題です。
こうした問題が出されると、他の学校でも、いろいろ工夫し始めます。
2012年度に出題された、聖心と白百合の問題は、形こそ違え、求めている考え方にはかなりの共通点が見られます。聖心の同じ値段のものを探す問題は、条件として示された、絵本と鉛筆と消しゴムの値段の関係の中で、「鉛筆2本が消しゴム4個と同じ値段」だというところを「鉛筆1本の値段は消しゴム2個と同じ」と理解できるかどうか、そこが問題です。
掛け算の考え方は、「一あたり量」×「いくつ分」で表されますが、その「一あたり量」の考え方が問われているのです。何を基本単位とするかを考えられるかどうかは、白百合の砂糖水の濃さでも問われています。水の量が半分になれば、砂糖の数も半分でよく、水の量が倍になれば、砂糖の数も倍にならなければ同じ甘さにならないという関係を理解できるかどうかです。遊びや生活で身に付けた直感を、いろいろな問題の解決に役立つ「考える力」にまで高めておくことが必要です。表面上一見異なるように見える問題も、それを解決する思考力には共通する面があるということをまわりの大人は知っておくべきです。だからこそ、ひとつひとつの問題を、試行錯誤させながら解かせることに意味があり、「この問題はこうして解きなさい」というような形だけの指導では、考える力の基礎は身につきません。
 
最近の入試で「考える力」がどこまで身についているかを学校側が見たいと考えていることは、以上の問題を見れば分かると思いますが、こうした問題の出題根拠は、一体どこにあるのでしょうか。多くのこうした問題を分析していくと、やはり小学校で学ぶ文章題、とくに高学年の文章題で求められる思考力が、その根拠があるように思います。では、こうした問題の対策はどのようにすればよいのでしょうか。
1 まず、子どもがどのように問題を捉え、解決しようとするかじっくり確認する
2 子どもの間違いには必ず原因があり、何を解決すればその高い壁を乗り越えられるかどうかを考えてあげる
3 考える力は、ペーパー学習のみでは身につかない。ペーパー学習の前に、試行錯誤ができるように、具体物や、カードを使った学習を積み重ねる
4 考え方の根拠が身についたかどうかを確認するために、答えの根拠を必ず説明させる
5 最後に、ペーパー学習を繰り返し、応用力を身につける
難問であればある程、自分で考える経験、物事に働きかけ、作業等を通して正解を導き出す経験をたくさん積むことが重要です。とかく、最初からペーパーだけを使った過去問トレーニングになりがちですが、それでは、学校側が工夫する「はじめての問題」に対応できません。「考える力」が求められる問題の対策は、学習の方法を工夫すること、つまり「事物教育と連動した学習」によって解決していくしかありません。
最新 久野先生のコラムはこちら (こぐま会HP 室長のコラム)
こぐま会教材はこちら
推薦コラム
|
| おけいこカードを使った学習法(54)
こちら |
| 子どもはどこでつまずくか(31)
こちら |
|
☆こぐま会トピック
・新ブランド! 『100てんキッズ』 こちら
・書店会員セミナー
こちら
|
|

