|
第9回
9月からスターとしたこぐま会の受験対策クラスの授業も、3月から基礎段階の最後である「ステップ4」に進みました。今年秋に受験される皆さんも、基礎段階の学習もほぼ終え、4月以降は、実際に出題された「過去問」のトレーニングに入っていくと思います。自分の力で考えなくてはならない問題が多い最近の入試問題を見るにつけ、基礎学力をしっかり身につけておかなければなりません。あせって、ペーパーのみの「過去問トレーニング」だけでは、基礎学力は身につきません。
数における基礎学力は、将来の四則演算につながる内容を、生活場面に合わせて学ぶことですが、最大の課題は掛け算の考え方の基礎となる「一対多対応」の学習です。2013年度の入試でも、多くの学校で出題されています。例えば、次のような問題です。
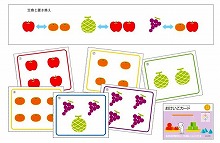
K校(2013年度)【一対多対応】
・子どもたちが下に落ちているドングリを2個ずつお土産にするには、あといくつリスにドングリを落としてもらえばいいですか。
その数だけ下のお部屋に○をかいてください。
|
|
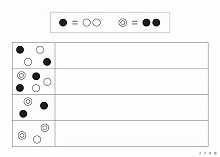
S校(2013年度)【一対多対応と交換】
上のお部屋を見てください。
●は〇2個に換えられます。◎は●2個に換えられます。
・それぞれのお部屋にある印を全部○に換えると、○はいくつになりますか。その数だけ右のお部屋に青い○をかいてください。
|
|
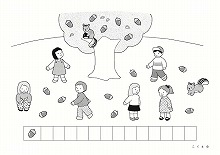
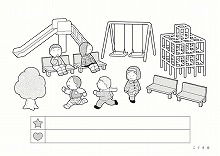
D校(2013年度)【数の増減と一対多対応】
子どもたちが公園で遊んでいます。
・今公園にいる子どもたちに、アメを3個ずつ配りたいと思います。アメはいくついりますか。その数だけ星のお部屋に○をかいてください。
・しばらくすると2人の子どもが帰り、またすぐに3人遊びにやって来ました。その後1人帰りました。今公園にいる子どもたちにリンゴを2個ずつあげるには、リンゴはいくついりますか。その数だけハートのお部屋に○をかいてください。
|
|
単純な一対多対応の問題と、それを応用した「つりあい」や「交換」の問題とがありますので、学習する順序を間違えないで行う必要があります。
上記1の内容は「お客さんが4人来ました。ひとりに3枚ずつお煎餅をあげるには、全部で何枚あればよいですか」という基本問題が解れば問題なく解けるはずです。しかし、2のような問題になると、「置き換え」の発想が必要となり、思考力が要求されます。
◎と●の関係、●と○の関係を踏まえ、すべて○に変える問題ですが、交換の問題としては、かなり基本の問題です。
私が、40年間の受験指導の中で、一対多対応に関する一番難しいと感じている問題は、以前紹介した、雙葉小学校のハンバーガーに関する交換の問題です。
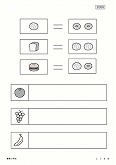
雙葉小学校(2008年度)【交換】
上のお部屋を見てください。
メロン1個は、ドーナツ2個と換えてもらえます。 食パン1斤は、メロンパン2個と換えてもらえます。
ハンバーガー1個は、メロンパン1個とドーナツ1個と換えてもらえます。
・メロンパン4個は、食パンいくつと換えてもらえますか。その数だけリンゴのお部屋に○をかいてください。
・食パン2斤は、ドーナツいくつと換えてもらえますか。その数だけブドウのお部屋に○をかいてください。
・ハンバーガー4個は、食パンいくつと換えてもらえますか。その数だけバナナのお部屋に○をかいてください。
|
|
この問題は、毎年父親の集まりである「土曜ゼミ」で実際に解いてもらっていますが、大人にとっても難しい問題です。
何が難しいか?
難しくしている最大の要因は、「ハンバーガー1個は、メロンパン1個とドーナツ1個に換えてもらえる」という約束です。従来の問題のほとんどが、交換条件の数こそ違え、一種類のものと一種類のものが交換できる条件ばかりでしたが、この問題は、一種類のものが二種類のものと交換できるとなっています。こうした交換条件は初めてだと思います。そのため、最後の問題が難しくなるのです。
ちなみに、最後の問題を受験間近な子どもたちに出題しても、三分の一ぐらいの子どもしか正解できません。どんな答えが出てくるかというと、「2」「4」「6」といった答えが見られます。
なぜそうした答えになったのか、一人ずつ説明させると、間違えてしまった理由は必ずあります。その間違いを一人一人正してあげれば、必ず正解の「3」にたどり着きます。あと一歩の作業が足りなく、正解に至っていないのです。
では、この雙葉の問題をどのように学習したらよいのか、具体的にお伝えしましょう。
それは、同時に「一対多対応」の学習の仕方につながりますので、ぜひ順序を踏まえて学習してください。この問題は、原則として、3つの段階を踏まえて学習します
。
1−A メロンパン3個はドーナツいくつと換えてもらえますか
1−B ドーナツ8個は、メロンパンいくつと換えてもらえますか
2−A 食パン2斤は、ドーナツいくつとかえてもらえますか
2−B ドーナツ8個は、食パン何斤と換えてもらえますか
3−A ハンバーガー4個は、食パン何斤と換えてもらえますか
3−B 食パン3斤は、ハンバーガー何個と換えてもらえますか
1のA・Bの段階は、単純に一つの約束をもとに、問いかける問題ですが、Bのように逆から聞くこと(割り算の包含除)も忘れないでください。
メロンパンからドーナツを聞く問題だけを練習していると、逆から問いかける問題に答えられない場合が出てきます。
2のA・Bは、あるものに一度置き換えて練習する課題です。この場合、メロンパンに一度置き換えて考える問題です。この考え方は、シーソーのつりあいの難しい問題の解き方につながっていきます。
最後の3のA・Bの問題が一番難しいはずです。子どもたちの考え方に沿って解説してみると、典型的な間違いは「4」と答える子どもです。この子は、次のように考えて「4」としてしまうのです。
1 ハンバーガー4個は、メロンパン4個とドーナツ4個に換えられる
2 メロンパン4個は、食パン2斤
3 ドーナツ4個は、メロンパン2個
ここまでは全く問題なく正しいのですが、ここで止まってしまい、2と2で4個としてしまうのです。ドーナツを変えたものがメロンパンであるということがしっかり意識できていれば、もう一度そのメロンパン2個を食パン1斤に換え、合計で3斤となるのに、あと一歩のところで止まってしまっているのです。4は正解ではありませんが、正解にかなり近いところまで考えが及んでいるのです。
「間違いには必ず原因がある」・・・これを我々大人は肝に銘じておくべきです。
どこで間違えてしまったのかを見つけ、子どもの思考に沿って修正してあげれば、この難しい問題も解決に至るのです。「2」と答えた子どもは、ドーナツを捨ててしまった子ども、6と答えた子どもは、ドーナツの数をそのまま、食パン2斤と合わせてしまった間違いです。やはりドーナツの処理に問題があるのです。
「3」という正解に至った子どもも、最初にドーナツ4個をメロンパン2個に換え、メロンパン6個を食パン3斤に換えた子はほとんどいません。多分、メロンパンが出た段階で、すぐに約束が目につき、まずメロンパン4個を食パン2斤に換えてしまうのでしょう。子どもらしい発想がそこに見られます。
一対多対応の問題は、入試における数の問題の中心になっていますし、「つりあい」や「交換」といった難しい問題に応用されていきます。
今回は、雙葉の問題を素材に、その学習法をお伝えしましたが、段階を踏んで学ぶ一つの典型として実際にやってみてください。
(注)「一対一対応」の言葉は辞書を引けば出てきますが、「一対多対応」の言葉は、辞書を引いても出てきません。これは、私が「ひとりでとっくん」シリーズの問題集を作る際に、「一対一対応」にならって「一対多対応」と命名した造語です。
最新 久野先生のコラムはこちら (こぐま会HP 室長のコラム)
こぐま会教材はこちら
推薦コラム
|
| 室長コラム 第247号「応用段階を迎えた子どもの学力の現状2 一対多対応の応用」
こちら |
| 教育レシピひとりでとっくん365日編45「つりあいの入ったシーソー・置き換えの考え方」
こちら |
|
☆こぐま会トピック
・新年長児対象「春季室長特別講座」 こちら
・新2歳児〜新年長児対象「体験授業」 こちら
・新年長児対象「暁星小学校対策クラス体験授業(大森教室)」 こちら
|
|
![]()

![]()
